√ 平面図形の重心 実験 411238-平面図形の重心 実験方法
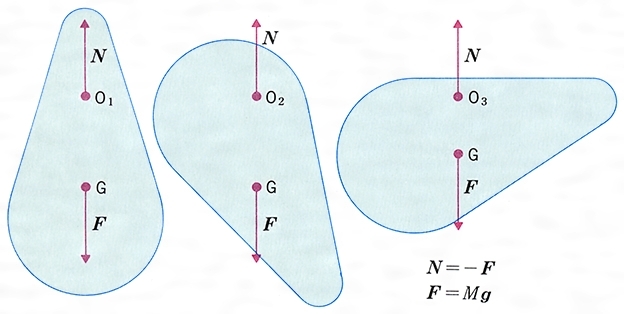
それなりの『定量実験』としても 耐えられるようにしていきます。 まず,基本は一様で均質な平面図形として三角形の板からはじめましょう。 重心は, 物体を一点でつるすとき,その物体の重心はその点の鉛直下方にある(2)空間図形を直線や平面図形の運動によって構成されたものとして捉えたり、平面上の表 現から空間図形の性質を読み取ったりすることができる。 (数学的な見方や考え方) (3)いろいろな立体を見取図や投影図、展開図に表すことができる。実験(イ) は, 図4 のように2 枚の板をつるし, 糸を動かして,釣り合う位置を求めるものであ る。本授業において,図形の重心の定義を「図 形をある1 点で支えると釣り合う(水平に静 止した状態で支えられる)とき,その点をその 図形の重心という。」とした。
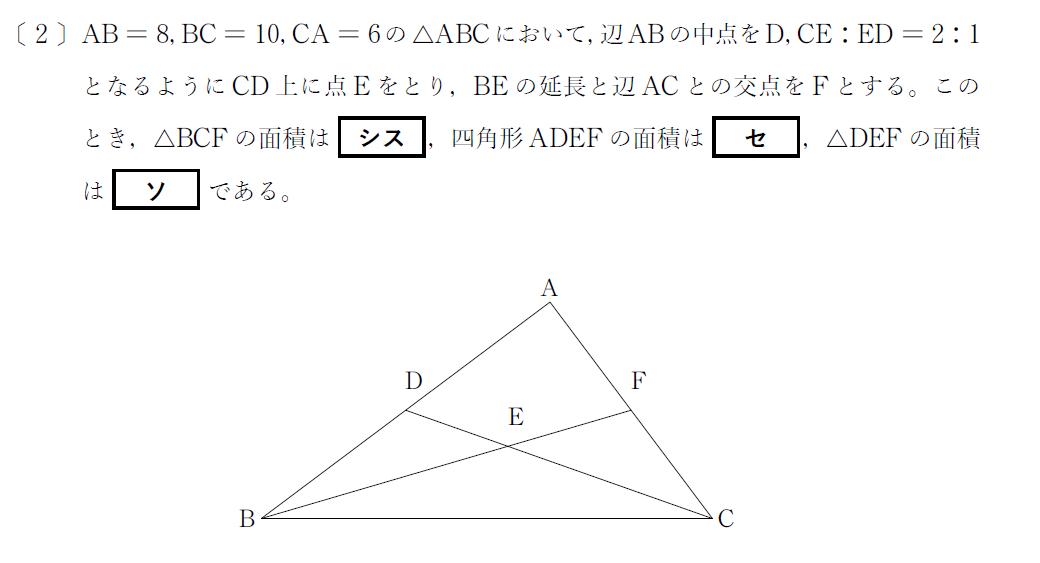
三角形の重心と面積に関する問題です F1 数学 箱根駅伝ブログ
平面図形の重心 実験方法
平面図形の重心 実験方法-Q1 重心とは何か。 Q3 ある平面図形の重心を探すにはどうすればよいか。 ある平面図形の重心を探すにはどうすればよいか。 制作・著作/NHK (Japanもしも、重心からの鉛直線が底面を通らなかったとすると、図12の左側の状況になり、右側にあるように立ちます。 これらの状況から、 立っているということは、重心からの鉛直線が底面を通るということ になります。



2
数学A /図形の性質「平面図形」 5 / ??①の図形は、 です。 ②の図形は、 です。 全断面積は、 a=2××10=36 です。 よって、y方向の図心位置は y= ()/36=677⇒68cm です。 x方向の図心位置も上記と同様の方法で算定できま数学の分野でも、図形や平面幾何の分野で重心というものが出てきます。 平面幾何学で登場する図形には重さなどの概念がないため、上記の公式のすべて質量に 1 を代入したものが、数学で習う重心の公式になります。
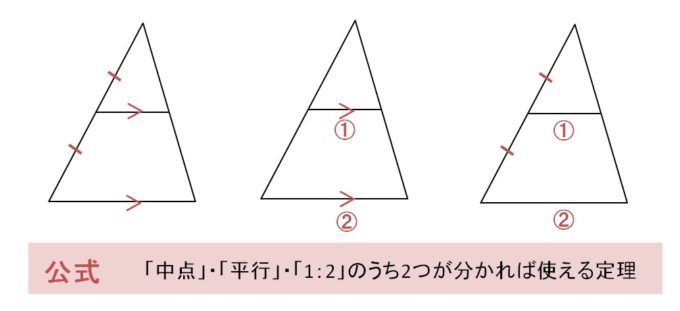
実験的な求め方(分割形状の重心が不明?) ①平面図形の1 点に小さな穴1 をあけ て糸でつるし,穴の中心から鉛直下 向きに線を引く。 ②違った位置に穴2 をあけて糸でつる し,穴の中心から鉛直下向きに線を 引く。 ③二つの直線は重心を通るので,2 直積分表示になっているので難しそうに見えますが、結局のところ求めるべきは加重平均なので、考え方は変わりません。 質量分布が一様な物体であれば、今回紹介した公式 x G = ∫ 0 L f ( x) x d x ∫ 0 L f ( x) d x を用いて複雑な図形の重心であっても求めること相似を表す記号 4ABC と4DEF が そうじ 相似のとき 4ABC ˝ 4DEF と表す. 三角形の相似条件 a b c ka kb kc a b ka kb 三角形が相似になる条件は次である. 1 3 辺の辺の比がすべて等しい ˆ 相似比1 k 2 2 辺の辺の比とその間の角がそれぞれ等しい ˆ 相似比1 k
や実験などの活動を通して,見通しをもって作図したり図形の関係について調べたりして面図形につ 面図形の単元では,意欲や関心を持って学習に取り組んでいる生徒が多い。 事前に行った小テストで 平面図形 予想した結果を確認したりするなど丸く重心が下の方にある(底の曲率中心より重心が下 にある)からである。そこで、写真11のようなモデルを用 意した。ではなぜ底が丸く重心が下の方にあれば起き 上がるのかであるが、ここでは重心の位置に注目した。③平面図形の性質の調べ方には実験 ③平面図形の性質を既習内容と関連 ・実測による方法や証明による方法 付けて、体系的にとらえることがで があることや,証明による方法の楽 きる。 しさに気付く。



四角形の重心のちょっとした誤手技



おもしろ数学講座
2 平面体の重心 物体がいくつかの質点からなり、質点の質量をm1、m2、m3、・・・とする。(図1) このとき物体の重心Gの位置(xG、yG)は次式で表される。三角形 の頂点 におもり を1個ずつ つるした の場合 、三角形 の面重心 (三角形 の板自身 の重心 ) と3カ所のおもりの 重心 が一致 するため 、実験 で得たつりあう 点は中線 の交点 となっている 。 そのため 、容易 につりあう 点を推測 することもできる 。- 「直線と平面の位置関係」におけるコンテンツ開発とその活用を通して - 七ヶ宿町立七ヶ宿中学校 川村 陽一 概要 中学校数学の図形領域では観察,操作や実験を通して図形の概念や性質の理解を図っ ていくことが目標とされている。
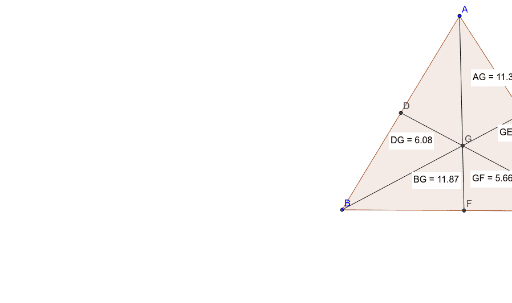



平面図形 三角形の性質 重心 Geogebra
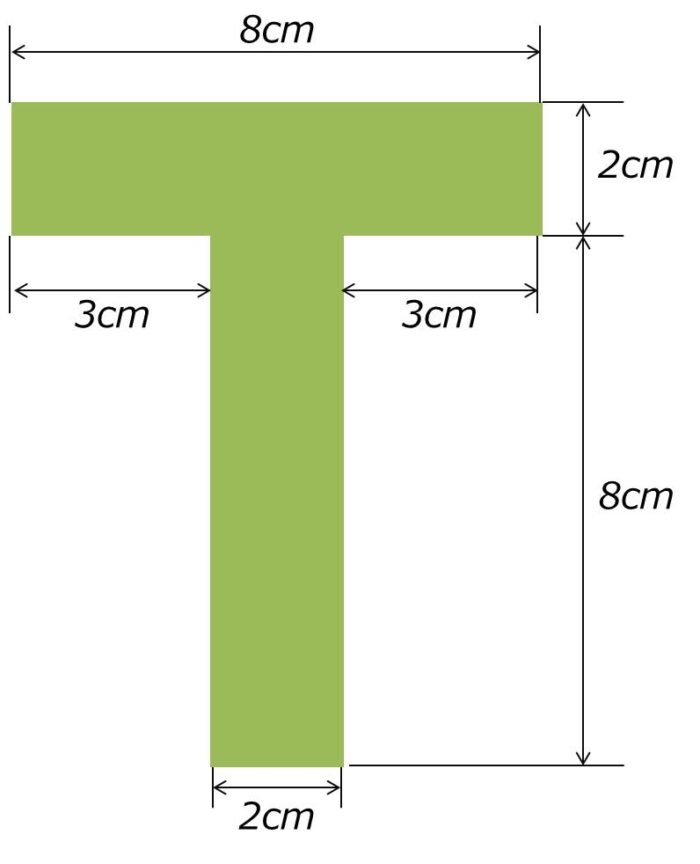



構造力学 断面1次モーメントを用いて図形の図心を求める
こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の重心」 の座標・位置ベクトルの求め方や、その公式の証明、また重心の重要な性質を利用した面積比を求める問題などをわかりやすく解説していきます。 また、記事の後半では、三角形重心の求め方について この場合,厚さ一定であるから、2次元平面で考えることができる。 t型の場合 図形の形状が、重心の位置が既知の図形に分解できるときにはそれぞれの面積と位置から合成することにより全体の形状の重心位置が求められます。1 単元名 「平面図形」(教科書:日本文教出版) 2 単元の目標 観察、操作や実験などの活動を通して、見通しをもって作図したり図形の関係について調べたりし て平面図形についての理解を深めるとともに、論理的に考察し表現する能力を培う。



2



おもしろ数学講座
目指すは理系爺・・・ 高校数学目次 平面ベクトル ベクトルと平面図形 ベクトルと平面図形 位置ベクトルとは? 位置ベクトル関連問題 内分 外分 重心 位置ベクトル 内分 外分 重心 練習問題 練習29:三角形の重心の位置ベクトル重心の求め方 いろいろ 実験 長方形の紙を2つに折り,90°位の角度に開いて机の上に置く。その折り目の上に硬貨を乗せ,紙を静かに開いていくと,紙がほぼ平面に近く広がっても硬貨は落ちない。図形の重心に対する感覚を豊かにする教材の提案 ~正方形,長方形,l 字型図形の重心を見つける活動を通して~ 納土恵美香¹,山路健祐²




Ppt Belle 実験の最新結果 08 年夏 Powerpoint Presentation Id




複雑な図形の重心 平面図形の重心の決定
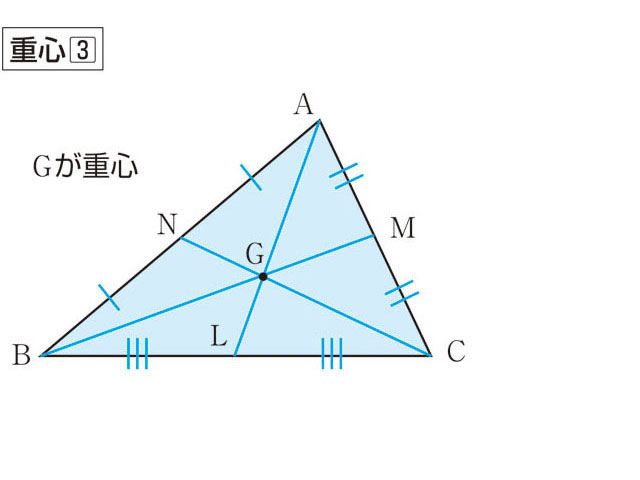
いの状態を保つ。図2c のように切り取ると、重心の鉛直 下方向に接地面がなく、左方向に回転する。 図 2 物体の底面を削ったときの回転について 以上のように、物体の重心が、その物体の接地面から出 たとき回転する。三角形の垂心 図の ABCをみてください。 ABCの各頂点から、それぞれ対応する辺に垂線がひかれています。不思議とこの3本の垂線は1つの点で交わり、この点のことを垂心と呼びます。 三角形の重心 図の DEFをみてください。 三角形の各辺を(板の重心) 多角形の内部すべてに,均一の重さがかかっている場合の重心 が考えられる。最も一般的には,多角形の重心といった場合は,「多角形板の重心」のことで ある。 ※三角形abcの中線の交点をgとする(この点gを三角形abcの重心という)。この



Oyama Ct Ac Jp



2
科目名・単元名 数学a・平面図形 使用教材 教科書 折り紙 厚紙 単元の目標 三角形や円などの基本的な図形の性質についての理解を深め、図形の見方を 心は 線を : の比に 内分する。」 <実験>厚紙から切り取った三角形を ・重心の意味が理解でき重心とは、物体の重さが作用する点です。 普通、重力は一様に作用するので、図形の芯が重心であることが多いです。 今回は重心の簡単な意味、定義、求め方、公式について説明します。 下記の記事を読むと、スムーズに理解できます。 図心ってなに生徒実験:平面図形の重心 1目的 幾何学的図形の重心の位置を実験で求め、計算結果と比較する。 2原理 物体を任意の点で固定し、重力のもとで自由に回転できるようにすると、重心 がその固定点の真下にきたときにつり合って静止する。
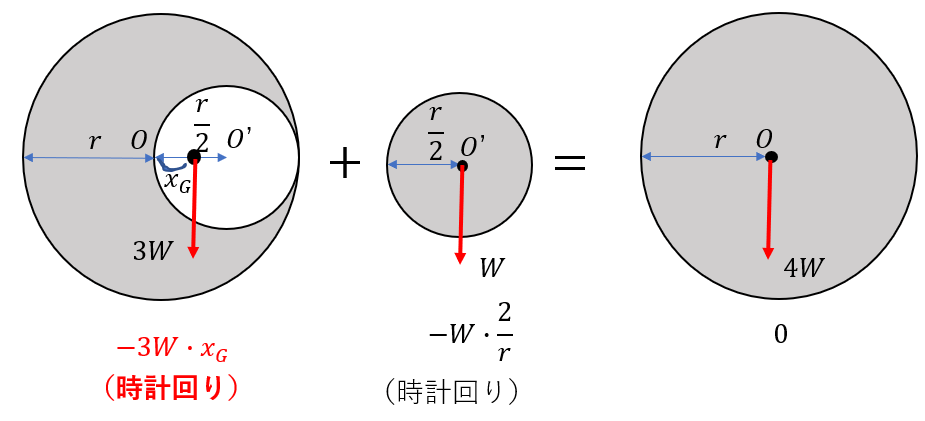



円の切り抜き図形の重心の求め方 公式 そんなの使わんよ 受験物理 Set Up




単純閉曲面に囲まれた図形の重心1 中学3年生数学教科書からの三角形の重心についての証明問題 身勝手な主張
サイト運営者 直江津中等教育学校 堀江 光典 Mitsunori Horie重心の求め方から応用問題まで徹底解説! │ 受験スタイル 例題付き重心って何? 重心の求め方から応用問題まで徹底解説! なんとなく物体の中心というイメージをもっているのではないでしょうか? 物理基礎でもあまり説明なく、そのように重心 高校物理では, 質量はあるが大きさは無視できる という 質点 についての議論がもっぱらである しかし, 現実の物体はゼロでない大きさを持ち, 物体内部で質量の分布に 斑 ( むら ) もあるであろう このような現実的な物体を議論する場合において




数学教室のバックナンバー 雑誌 定期購読の予約はfujisan
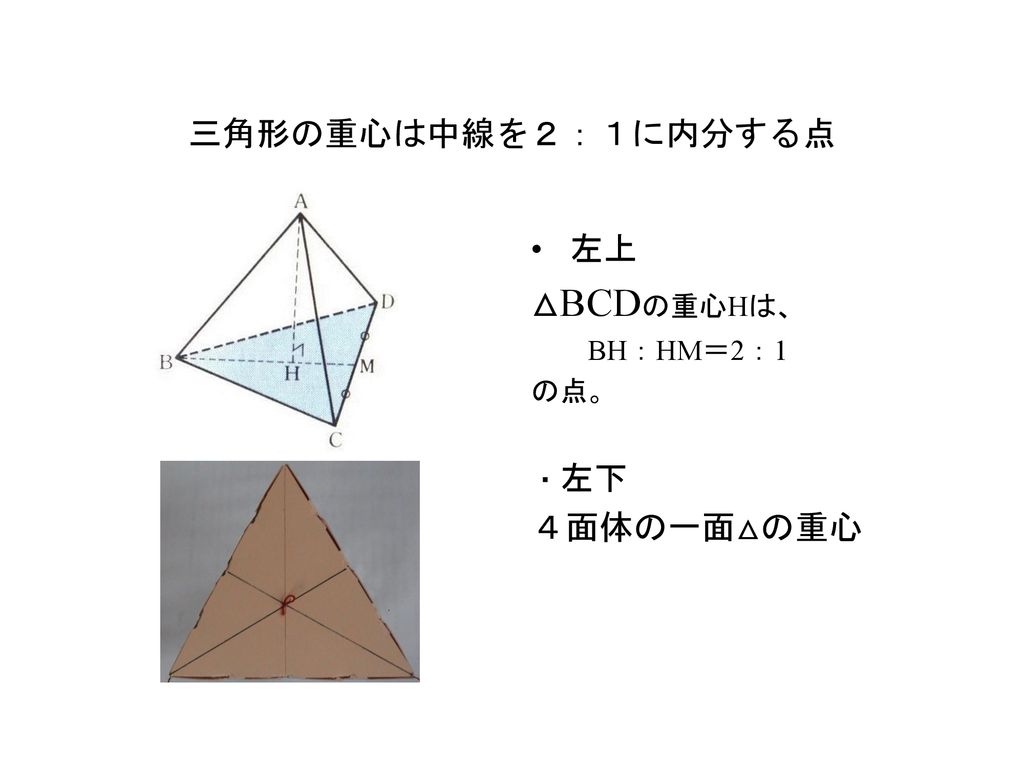



4面体 正3角錐 の重心 重心を透視できる4面体づくり Ppt Download
平面図形の重心の問題に自然に移行させていく(図5)。 ここで,重りの場合と異なる注意として,図5のF型の ように部分的にえぐれていて,正方形が上下ではなく横 で繋がっている図形の取り扱いである。この場合もモー(2) 平面図形や空間図形についての観察,操作や実験などの活動を通して,図形に対する直観的な見方や考え方を深めるとともに,論理的に考察し表現する能力を培う。 (3) 具体的な事象を調べることを通して,比例,反比例についての理解を深めると今年の4月、異動になりました。 新しい学校は前の学校とは全く違い、まさに異世界そのものです。校種が違うとこんなにも違うのか日々実感しています。トライアンドエラーの毎日です。 さて、新しい学校で4月の最初の生徒実験です。重心のお話。 実験:板をずらしながら重ねてい
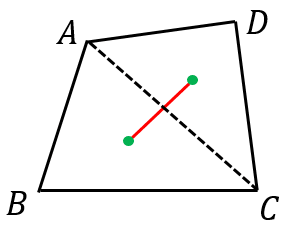



四角形の重心の2通りの求め方と注意点 高校数学の美しい物語




高校物理 難問にこそ現れる 重心 力学 お茶処やまと屋
よっ! くぎの出初め式 (No185) 実験監修:東海大学教育開発研究所所長 滝川洋二 ※監修者の役職は掲載当時のものです。 企画制作: 日本ガイシ株式会社 なんでだろう? マーカーペンの上に、数十本のくぎがバランスよくのっています。 まるで消防物体の重心の見つけ方 目的 いろいろな形の物体の重心の見つけ方とその原理を知る。 準備 工作用紙、糸、おもり、はさみ、定規、千枚通し、つまようじ;例えば、図3 の三角錐を、xy 平面で切った三角形の重心を求めると します。やはりf(x) = a h x で、S = 1 2 (2a)h = ah ですから、 xG = 1 ah Z h 0 x 2 a h xdx = 2 h2 Z h 0 x2dx = 2 h2 1 3 h3 = 2h 3 より、重心は頂点より 2h 3 の位置または底辺より h 3 の位置と表せま す。 例題 半径a



図心ってなに 図心の求め方と断面一次モーメントの関係



全2問 画像の図形の重心 質量中心 は 仲良く平等に分けなさいよ Jyankquiz
をその図形の「重心」という 。 図形を吊るす場合で言えば,図形の「重心」 は,図形をその上のいろいろな点から吊るし たときのそれ らの吊るす点を通る垂直線の 交点である 。 そうすると,点対称図形に関しては,その 重心の位置が直ちに求められる



2




例題付き 重心って何 重心の求め方から応用問題まで徹底解説 受験スタイル



放物線と重心 物理実験集 管理人の近況報告ブログ




ラッピング無料 誕生日 クリスマス プレゼントに大人気 ボーネルンド マグ フォーマー 正規品 マグフォーマー 追加パーツ 長方形セット 磁石 ご予約品 知育玩具 ナチュラルリビング マグネット あす楽対応 ブロック Bornelund 12ピース ジムワールド社 パズル




切り抜かれた円盤の重心 高校物理の備忘録



2



2




単純閉曲面に囲まれた図形の重心1 中学3年生数学教科書からの三角形の重心についての証明問題 身勝手な主張




数学a 平面図形 重心 オンライン無料塾 ターンナップ




16年京大理系第三問 見掛け倒しの図形論証 数学アマノジャク
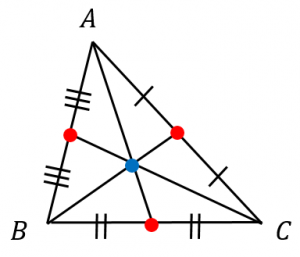



三角形の重心の定義といろいろな求め方 具体例で学ぶ数学



東京都の重心へ行ってみた 俺の居場所




水理学演習 上下巻セット メルカリ



1
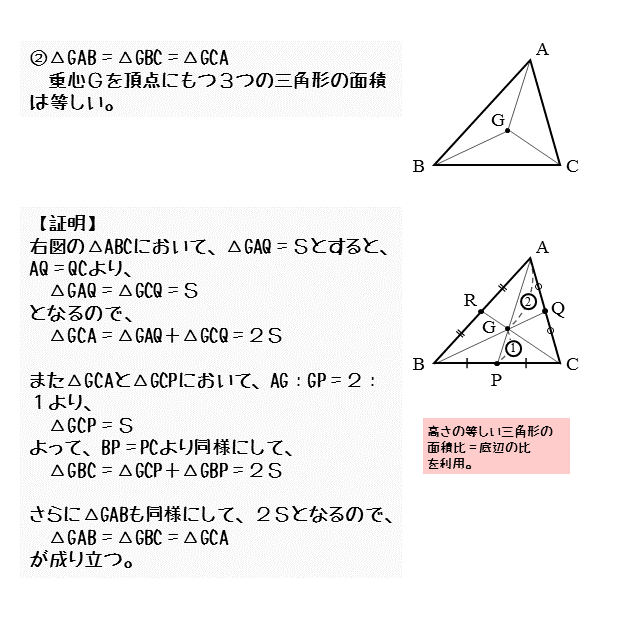



図形の性質 重心について 日々是鍛錬 ひびこれたんれん



平面図形の重心を実験的に調べるにはどうのような方法があります Yahoo 知恵袋



実験と実験器具 物理実験集 管理人の近況報告ブログ




図形の重心を解析的に求める方法 理系のための備忘録



2 刺激の位置や提示時間の指定方法を覚えよう Psychopy Builderで作る心理学実験 4 1 1 ドキュメント



重心 わかりやすい高校物理の部屋




図形の重心を解析的に求める方法 理系のための備忘録
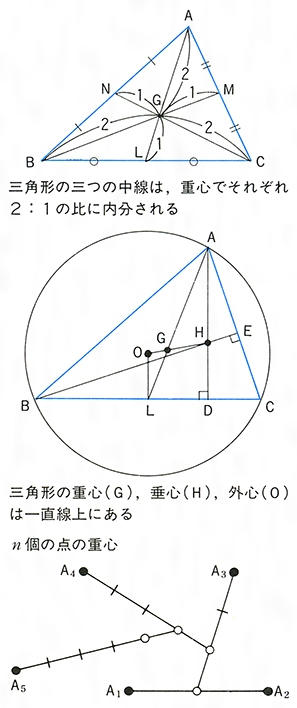



重心とは コトバンク
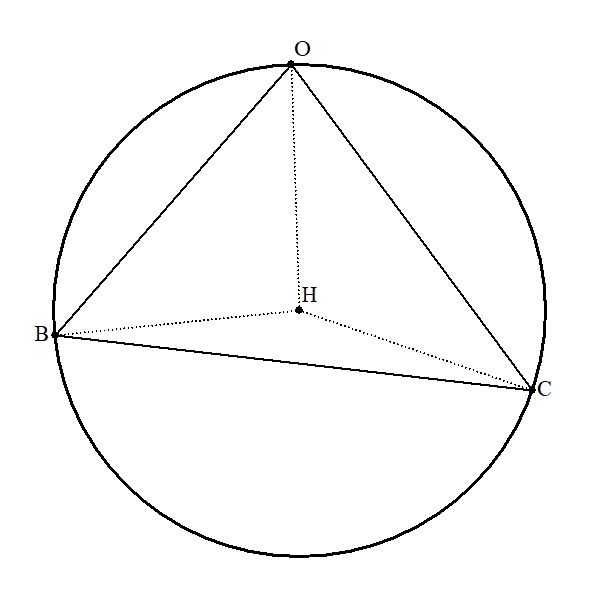



16年京大理系第三問 見掛け倒しの図形論証 数学アマノジャク



重心とは コトバンク



図心の求め方




ラッピング無料 誕生日 クリスマス プレゼントに大人気 ボーネルンド マグ フォーマー 正規品 マグフォーマー 追加パーツ 長方形セット 磁石 ご予約品 知育玩具 ナチュラルリビング マグネット あす楽対応 ブロック Bornelund 12ピース ジムワールド社 パズル



2 刺激の位置や提示時間の指定方法を覚えよう Psychopy Builderで作る心理学実験 4 1 1 ドキュメント




三角形の重心と面積に関する問題です F1 数学 箱根駅伝ブログ



高校入試対策数学 三角形の重心の演習問題 Examee




単純閉曲面に囲まれた図形の重心1 中学3年生数学教科書からの三角形の重心についての証明問題 身勝手な主張




Stress Distribution During Cold Compression Of Rocks And Mineral Aggregates Using Synchrotron Based X Ray Diffraction Protocol Translated To Japanese



平面図形の面積 周長 重心位置の求め方



Www2 Matsue Ct Jp



2



2




第3弾理科実験イベント 重心って何 バランス名人になろう には 小1 小4の 京丹波町の科学教育を推進支援する会 Facebook



2



図心ってなに 図心の求め方と断面一次モーメントの関係



2



Core Ac Uk



御所実業高校 機械工学科 の日記 第21回 重心 2 問16の解説



ゆうメール利用不可 実験動物発生異常アトラス 外表異常 日本先天異常学会用語 Drrayyoong Com Au




例題付き 重心って何 重心の求め方から応用問題まで徹底解説 受験スタイル



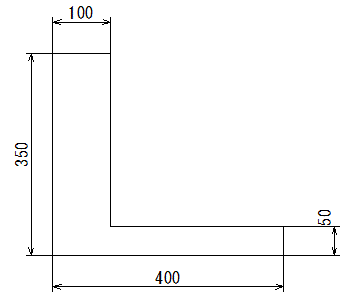
重心 図心の求め方こんなやり方で何で求まるの h型の平面図形の重 Yahoo 知恵袋



2



重心とは コトバンク




重心とは何か 座標を使って重心を求める方法 物理 高校生向け受験応援メディア 受験のミカタ



時間認識という錯覚 増補版 時間の矢の起源を求めて



図心の求め方
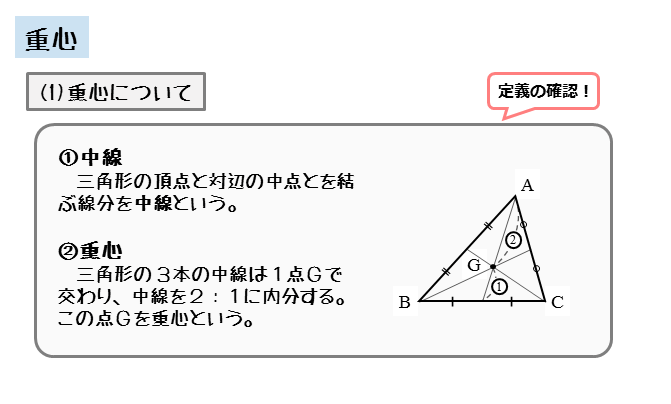



図形の性質 重心について 日々是鍛錬 ひびこれたんれん



Ngas E Chiba U Jp



2



やさしい実践 機械設計講座




ガードナーの楽しい実験 芳賀サイエンスラボ




よっ くぎの出初め式 自由研究におすすめ 家庭でできる科学実験シリーズ 試してフシギ Ngkサイエンスサイト 日本ガイシ株式会社



大至急 コイン100枚 この平面図形の重心の求め方を教 Yahoo 知恵袋




06 号 液体吐出ヘッド Astamuse




重心 記号 重心 記号 パワポ




A 6 13 B 1 1 65 Y C 2 A 2 1 B 3 2 C 66 X 2y 1 0 2 A 1 1 B 3 0 P 67 3 A 3 3 B 1 2 C 4 0 1 Abc G 2 3 A B C P 6



工業高校に通っている高校生です 明後日テストがあるのですが 平面図 Yahoo 知恵袋




重心の位置を実験で求める方法 軽い平面形状物体 Youtube




16 号 実験動物の視機能評価装置 Astamuse




実は深い実験 重心で遊ぶ Youtube



Johnouchi Hs Tokushima Ec Ed Jp



2




実は深い実験 重心で遊ぶ Youtube



投稿155




図形の重心を解析的に求める方法 理系のための備忘録



物体の重心




重心とは何か 座標を使って重心を求める方法 物理 高校生向け受験応援メディア 受験のミカタ




物理学実験 A Manualzz




実験室系と重心系 高校物理の備忘録



2



大学入試問題




三角形の重心について知っておきたい知識まとめ 理系ラボ



工学の機械設計で質問です 平面図形の重心を求める問題です右図 Yahoo 知恵袋



四角形の重心のちょっとした誤手技




Woa1 パターン認識装置 Google Patents
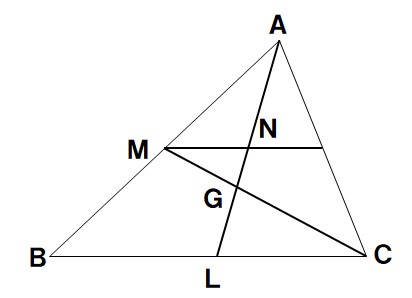



高校入試対策数学 三角形の重心の演習問題 Examee



2




Geogebra の記事一覧 数樂管理人のブログ
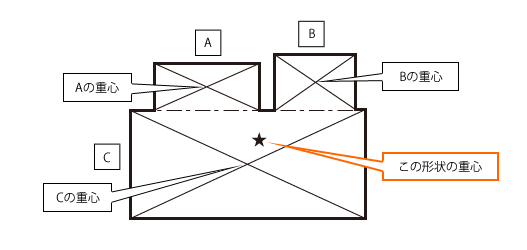



重心について 機械工学と自動機設計 8 技術情報 Misumi Vona ミスミ



2
コメント
コメントを投稿